
Part 1
- Problem 1: Create graphs
- Problem 2: Recommend by number of common friends
- Problem 3: Recommend by influence
- Problem 4: Does the recommendation algorithm make a difference?
- Reflection and submitting Part 1
Problem 1: Create graphs
It is always a good idea to test your code on a dataset that is small enough for you to compute the results by hand. You will create two such datasets for testing.
Problem 1a: A small practice graph
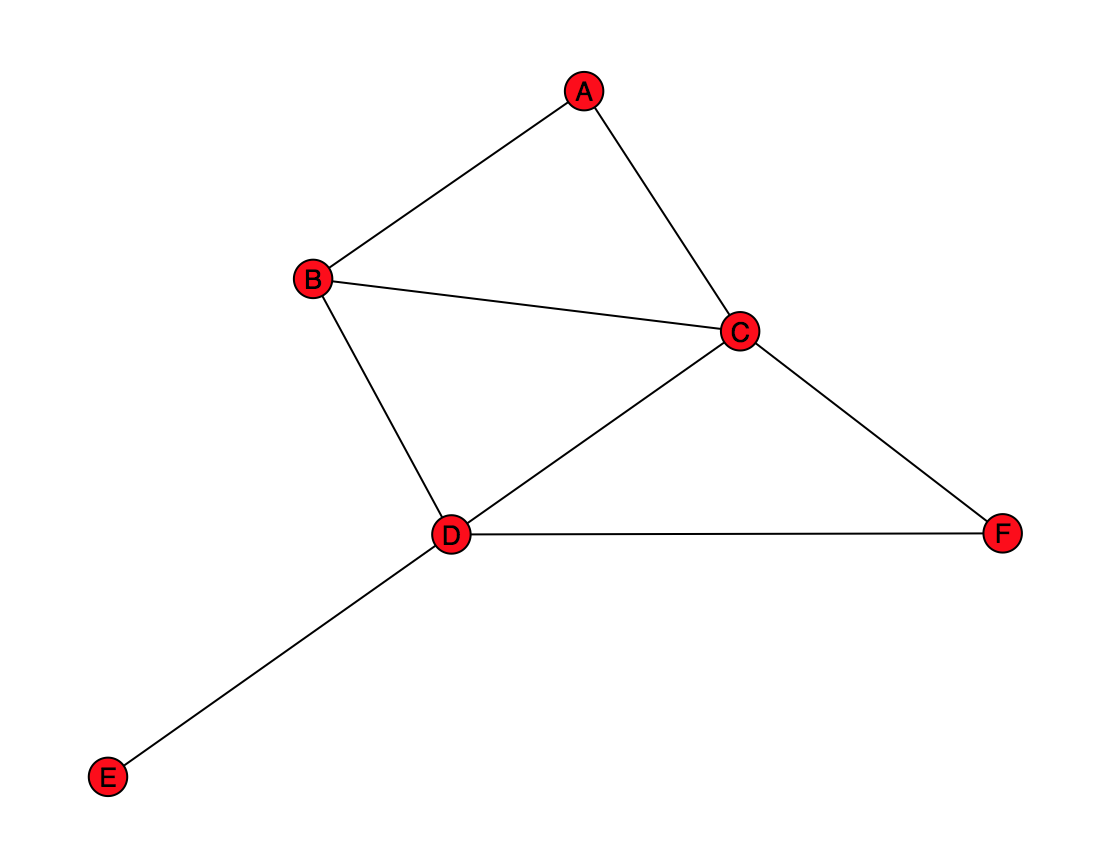
Above: a small graph containing 6 nodes, labeled A, B, C, D, E, and F
Create the above graph in get_practice_graph(). Note that there are letters inside each node (these may not show up in a printout of the assignment.) Use the Graph class as demonstrated in lecture (not DiGraph, MultiGraph, or MultiDiGraph).
To help you verify that your graph is correct, the provided code draws the graph to a window. The graph may be hidden behind other windows, so look for it! Compare your graph to the figure above.
Info
The nodes may appear in different locations; that’s fine as long as the same nodes exist and they are connected in the same way by the edges. If you redraw the graph, the nodes may be plotted using a different layout each time - this is also fine!
Important
Your program will pause until you close the window that contains the graph drawing.
When you are happy with your graph, comment out the call to draw_practice_graph() in the main() function at the bottom of the file (so you don’t have to close the window every time you run your program). Now look at the other .py file provided in the starter code: social_network_tests.py. This file has been set up for you to run when you are ready to test parts of your code. Run this test file with:
python social_network_tests.py
If you have drawn the practice graph correctly, you should see practice graph tests passed printed in the terminal. If you do not see this, consider looking at the error printed as well as the test function (test_practice_graph()) to figure out why your graph was incorrect. (You might also try writing some of your own tests to check your work!)
Once you have verified that your code passes the test, you should comment out the line in social_network.py where the practice_graph variable is defined, since you won’t need it for other homework problems.
Note
You are likely to see several other assertions in the test program failing after practice graph tests passed. This is to be expected since you have not yet implemented those parts of the program! In fact, this will continue to happen as you progress through the problems. This should not discourage you from regularly running social_network_tests.py to check your code. Success usually means you are no longer failing the same assertion, but that instead a different assertion is failing further down.
Problem 1b: The Romeo and Juliet graph
Create a graph in the get_romeo_and_juliet_graph() function corresponding to the Romeo and Juliet graph below (ignoring the shaded family/house information).
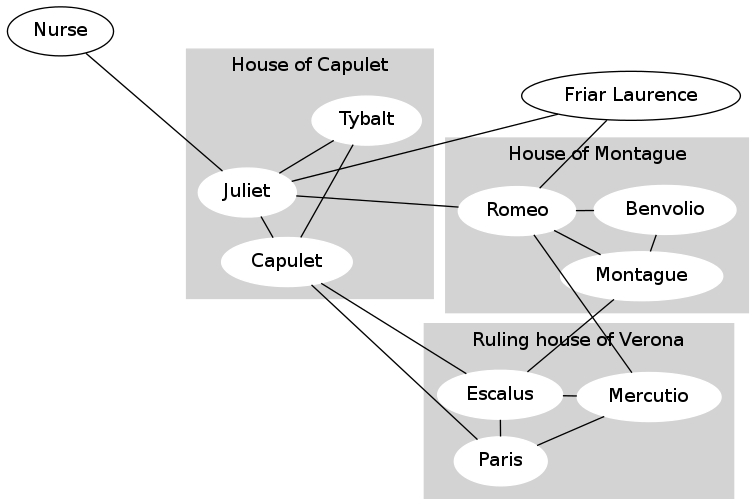
To help you verify that your graph is correct, the provided code draws the graph to a window and to a file named romeo-and-juliet.pdf. Compare your graph to the Romeo and Juliet graph above.
Info
The nodes may appear in different locations; that’s fine as long as the same nodes exist and they are connected in the same way by the edges. social_network_tests.py will check this for you.
When you are happy with your graph and the romeo-and-juliet.pdf file, comment out the call to draw_rj() in the main() function at the bottom of the file, so you don’t have to close the graph window every time you run your program.
Problem 2: Recommend by number of common friends
If a non-friend “Y” is your friend’s friend, then maybe Y should be your friend too. If person Y is the friend of many of your friends, then Y is an even better recommendation. The best friend recommendation is the person with whom you have the largest number of mutual friends. In this problem, you will implement this heuristic.
As a concrete example, consider “A” in practice_graph (pictured again below). Suppose we are interested in giving person “A” recommendations of people that they might want to be friends with. By this algorithm, the number of friends you have in common with someone is a measure of how likely it is that they would be a good friend recommendation for you. Therefore, the more friends someone has in common with you, the better their “friendship score” is. We will use the number of friends in common as the friendship score itself.

In this case, we want to find out who has friends in common with “A”.
- A has one friend in common with B (namely, C), but A and B are already friends, so we would not recommend B.
- A has one friend in common with C (namely, B), but A and C are already friends, so we would not recommend C.
- A has two friends in common with D (namely, B and C).
- A has no friends in common with E, so we would not recommend E.
- A has one friend in common with F (namely, C).
Because D has two mutual friends with A, D has a friendship score of 2 making D the top recommendation for A. Using the same logic, F is the second best recommendation. We would not recommend B or C because A is already friends with them. We also would not recommend E because A has no friends in common with E.

Similarly, consider Mercutio in the Romeo and Juliet graph.
- Mercutio has two friends in common with Capulet (Escalus and Paris).
- Mercutio has two friends in common with Montague (Escalus and Romeo).
- Mercutio has one friend in common with Friar Laurence (Romeo).
- Mercutio has one friend in common with Benvolio (Romeo).
- Mercutio has one friend in common with Juliet (Romeo).
- Mercutio has no friends in common with the Nurse, so we would not recommend the Nurse.
- Mercutio has no friends in common with Tybalt, so we would not recommend Tybalt.
Capulet and Montague are the best friend recommendations for Mercutio. Our algorithm should return this list ordered from best recommendation to worst. In the case of ties in friendship scores (such as between Capulet and Montague, or between Benvolio, Friar Laurence, Juliet), we list people alphabetically. Therefore, in this example we would return:
['Capulet', 'Montague', 'Benvolio', 'Friar Laurence', 'Juliet']
Important
We are not listing Paris, Escalus or Romeo because they are already friends of Mercutio.
The Algorithm
Now, let us think about how we might create this list. We will need to calculate these “friendship scores” for some set of people in the graph. Because we are using “number of common friends” as our metric, we only care about calculating scores for people who are friends of X’s current friends and not currently a friend of X.
There could be many people in a large graph, so we do not want to calculate friendship scores for every person in the graph. Many of those scores will likely be zero because they do not share any friends with X.
Because of this, we will need to calculate the set of “friends-of-friends” for user X. For each of those friends-of-friends, we will calculate the set of friends that they have in common with X. If we want to give user X a ranked list of recommendations from best to worst, then it would be useful to have a data structure to keep track of the mapping of “friend of friend” to friendship score. Finally, given this mapping of people to friendship scores, we will want to sort the potential friends from best to worst before presenting it to the user.
Tip
Remember that a dictionary is often called a “map”.
For this problem, you need to write the following five functions, whose documentation strings appear in the template file social_network.py:
friends_of_friends(graph, user)common_friends(graph, user1, user2)num_common_friends_map(graph, user)num_map_to_sorted_list(map_with_number_vals)rec_number_common_friends(graph, user)
Caution
Be sure to NOT modify any of the provided function definitions and arguments, as they will causes our autograder tests to fail
Tip
The template file defines a helper function, friends(graph, user), that you may find useful.
In the code we have provided, the bodies of all functions are empty except for a single statement: pass. This is a Python statement that does nothing, but can be used in situations where you need an instruction to be there but you don’t want it to do anything.
Note
In previous homeworks we instead wrote something like: # REMOVE THIS COMMENT AND REPLACE IT WITH YOUR CODE .... It is more common to see something like a single pass statement as a placeholder. Remove the pass statement when you have finished implementing the function.
The social_network_tests.py file contains several assert_equals statements and functions to help you test your code. We strongly encourage you to write additional assertions in these functions as well, in order to verify that your code is correct. You may also find the assertions useful for clarifying what the function is supposed to return. The function assert_equals(expected, received) takes in the first argument as the expected value, and the second argument as the actual value returned from the function. Like assert, this will stop your program if the two arguments aren’t equal.
Tip
For all of these functions, we strongly suggest that you start by outlining them in pseudocode.
Hints for Problem 2
Testing Dictionary Equality
Writing Additional Functions
Variable Naming
Hints for friends_of_friends and common_friends
Hints for num_map_to_sorted_list
Important
You are NOT allowed to use lambda. (If you don’t know what this means, that’s okay: you’re not allowed to use it anyways!)
Problem 3: Recommend by influence
In this problem, we will implement a different algorithm for computing a friendship score.
Consider the following purely hypothetical situation:
- Two of your friends are Margaret Hamilton and Anita Borg.
- Anita Borg has only two friends (you and one other person).
- Margaret Hamilton has 7 billion friends.
- Anita and Margaret have no friends in common (besides you).
Since Anita is highly selective in terms of friendship, and is a friend of yours, you are likely to have a lot in common with Anita’s other friend. On the other hand, Margaret has so many friends that there is little reason to believe that you should be friendly with any particular one of Margaret’s other friends.
Incorporate the above idea into your friend recommendation algorithm. We call this technique influence scoring. The drawing in this PDF depicts influence scoring graphically.
Suppose that user1 and user2 have three friends in common: f1, f2, and f3. In Problem 2, the score for user2 as a friend of user1 is 1+1+11+1+1. Each common friend contributes 1 to the score.
With influence scoring, the score for user2 as a friend of user1 now becomes:
In the example above, Anita’s one other friend would have a score of ½, and each of Margaret Hamilton’s friends would have a score of 1/7000000000.
Tip
We recommend that you calculate (by hand) the updated friendship scores for each of the friend recommendations that would be returned to Mercutio using this same metric. To see what the right answer should be, take a look at the assert_equals statement in the test_influence_map function in the file social_network_tests.py.
For Problem 3, implement two functions:
influence_map(graph, user)recommend_by_influence(graph, user)
The social_network.py file provides starter definitions for these functions, including docstrings. You may find that their implementations are quite similar to code that you have already written in Problem 2. That is OK. The social_network_tests.py file also tries one test case for each of the two functions. Do not change the code that you wrote for Problem 2. However, you can call many of the functions you wrote for Problem 2 to help with this problem.
Tip
You can solve the problem with just the two new functions (influence_map and recommend_by_influence), plus re-using some unchanged functions from Problem 2.
Problem 4: Does the recommendation algorithm make a difference?
Does the change of recommendation algorithm make any difference? Maybe not: you can see by looking at the assert_equals statements in social_network_tests.py that Mercutio should get the same friend recommendations with both recommendation approaches (see the functions test_recommend_by_num_common_friends and test_recommend_by_influence). Does that mean everyone gets identical results with the two recommendation approaches?
Using the Romeo and Juliet graph, write code to print a list of people for whom the two approaches make the same recommendations, then print a list of people for whom the two approaches make different recommendations. Each list should be sorted in alphabetical order. You do not need to write a separate function that does this, writing the code in the main() function is fine.
The format of this problem’s printed output is given in the Output Format section.
Tip
In the Romeo and Juliet graph, there are 5 people for whom the recommendations are the same, and 6 people for whom the recommendations are different.
Reflection and submitting Part 1
You are almost done with Part 1!
Submit social_network.py via Gradescope. You do not need to submit social_network_tests.py, even if you edited it.
Now you are done with Part 1! On to Part 2!